1. 🍅 문제
1654번: 랜선 자르기
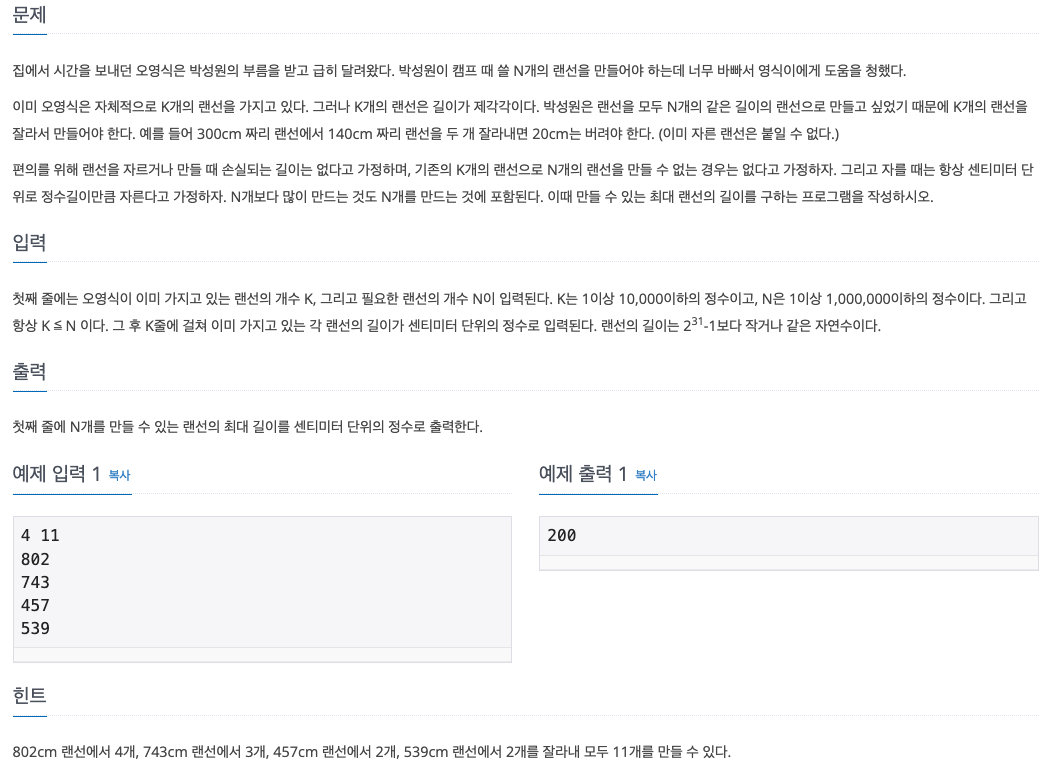
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
2. 🤔 어떻게 풀까?
이 문제는 이분탐색의 바이블같은 문제이다. 이분탐색 막 처음 배울 때 이 문제를 여러 번 봤었다. 나한텐 DP의 계단 오르기 문제와 같은 느낌이다. 아무튼! 어떻게 풀지 고민을 해보자.
문제를 요약하면 구해야 되는 것은 '주어진 K개의 랜선을 잘라 같은 길이의 n개 이상의 랜선을 만들 때 자를 수 있는 랜선의 최대 길이는?'이다. 결국 임의로 랜선의 길이를 설정하여 K개의 랜선들을 모두 잘라보는 수밖에 없다. 하지만 하나하나 자른다면 분명 시간초과가 날 것이다. 이렇게 범위가 크면서 하나하나 해보는 수밖에 없는 때는 바로 이분 탐색을 이용하면 된다.
1. 기준이 되는 값
이분탐색을 적용하기 위해 우선 기준이 되는 값을 뭘로할지 설정해야 한다. 우리는 최대 랜선의 길이를 구해야 하므로, 랜선의 길이를 기준 값으로 설정한다.
2. 랜선길이와 조각 수의 관계
두 번째로 랜선 길이에 따른 조각의 개수를 따져 봐야한다. 조금만 예제를 분석해보면 랜선길이가 클수록 조각 수가 작아지고, 랜선 길이가 작아질 수록 조각 수가 커짐을 알 수 있다. 이를 통해 left와 rigth를 조정한다.
3. 랜선 길이의 탐색 범위
세 번째로 랜선 길이의 범위를 설정해야 한다. 랜선의 길이가 가장 클때는 주어진 K개의 랜선 중 가장 큰 길이로 조각 수가 단 1개가 나오며, 랜선의 길이가 가장 작을 때는 1일 때이다. 코드롤 나타내면 다음과 같다.
3. 🖥️ 코드
`mid`는 자를 랜선의 길이가 된다. `mid` 값으로 k개의 랜선을 모두 나누어 잘라진 조각의 개수를 구한다. 이때 잘라진 조각의 개수가 N보다 크거나 같으면 `left = mid+1`로 만들고 현재 랜선의 길이가 최대인지 비교한다. 최대이면 `result`를 갱신한다. 이렇게 하는 이유는 N개의 조각 수를 만드는 것이 아니, N개 이상의 조각을 만들어도 랜선의 길이가 최대이면 되기 때문이다.
import java.io.*;
import java.util.*;
public class Main{
public static void main(String [] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int K = Integer.parseInt(st.nextToken()); // 가지고 있는 랜선의 수
int N = Integer.parseInt(st.nextToken()); // 필요한 랜선의 수
int [] lanCable = new int[K];
int max = 0;
for(int i=0; i<K; i++){
lanCable[i] = Integer.parseInt(br.readLine());
max = Math.max(lanCable[i], max);
}
long right = max;
long left = 1;
long result = 0;
while (left <= right){
// 랜선의 길이
long mid = (left+right)/2L;
long count = 0;
// 잘라진 랜선의 개수
for(int i=0; i<K; i++){
count += lanCable[i]/mid;
}
// N값보다 랜선이 많으면 랜선의 길이를 늘림
if(count>= N){
left = mid+1;
// 문제의 조건은 N개이거나 N개보다 많으면 됨
result= Math.max(result, mid);
}else{
right = mid-1;
}
}
bw.write(result+"\n");
bw.flush();
}
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 연구소 : 14502 : Java - 그래프 탐색 (G4) (0) | 2023.12.14 |
|---|---|
| [백준] 꿀 따기 : 21758 : JAVA (0) | 2023.12.09 |
| [백준] 쉬운 계단 수 : 10844 : Java - DP (S1) (1) | 2023.12.03 |
| [백준] 파일 합치기3 : 13975 : Java - 그리디 (G4) (1) | 2023.12.02 |
| [백준] 점프 : 1890 : Java - DP (S1) (3) | 2023.11.29 |